Your matrix will have rank 3 when its determinant is not equal to zero. For Bias vectors you are just looking at the size of the vector.

Solve A Linear Second Order Homogeneous Differential Equation Initial Va Differential Equations Solving Equations
I In the given matrix we have 4 rows and 4 columns.

. Number of parameters in a CONV layer would be. Row function in R Language is used to get the row number of a matrix. Out of these 6 equations only 4 equations contribute to the number of parameters and by looking at the equations it can be deduced that all the 4 equations are symmetric.
For fully connected layers the weight matrix W will have R x C parameters where R and C are the number of Rows and columns respectively. So all values of a are valid except any value s of a for which the determinant is zero. Shape of width of the filter shape of height of the filter number of filters in the previous layer1number of filters.
Hence the number of elements in the given matrix is 16. Find the number of parameters in AT if A is a 4 x 3 matrix of rank 2. Find the rank and nullity of matrix A A 1 4 -3 2 4 5 -2 2 5 1.
The dimension of the null space can be interpreted as the number of arbitrary parameters in the general solution to Ax 0 so the number of arbitrary independent. The rank is the number of nonzero rows of a reduced row echelon form matrix of the given matrix. The resulting matrix C AB has 2 rows and 5 columns.
Each zero row represents 1 parameter. Row x asfactorFALSE Parameters. A 3-fold cross-validation and hyperparameter selection study is going to be conducted to find out the best parameters for the MNIST dataset classification.
SVM is a supervised machine learning algorithm. A Symmetric full DxD covariance matrix giving DD - D2 D parameters DD - D2 is the number of off-diagonal elements and D is the number of diagonal elements 2. The colors here can help determine first whether two matrices can be multiplied and second the dimensions of the resulting matrix.
This is uniquely solvable as long as R and L are linearly independent. Simply do the math. The dimension of the null space of an m x n matrix A is n - rankA.
For example if A is a 2 3 matrix and B is a 3 5 matrix then the matrix multiplication AB is possible. So use your favorite method for computing the determinant to obtain a function in a set this function equal to 0 and solve. For instance requiring that a matrix be symmetric a_ij a_ji for j neq i means that you have n2 - nn-12 n2 - n22 n2 n22 n2 nn12 free parameters the upper triangle or lower triangle of the matrix.
In our project we aim to implement the SVM algorithm on the MNIST dataset handwritten digits dataset to classify digits using scikit-learn. M n d1 k added 1 because of the bias term for each filter. If R and L are not linearly independent then your equation is M D R where D A B and you are back to having an infinite number of solutions.
Therefore there will be 4 parameters. Soif we find out the number of parameters for 1 equation we can just multiply it by 4 and tell the total number of parameters. Free matrix calculator - solve matrix operations and functions step-by-step.
That is C is a 2 5 matrix. If you limit A and B to multiples of the identity matrix your equation becomes M a R b L where a and b are simply numbers. LSTM parameter number 4 x h h h LSTM parameter number 4 3 2 2 2 LSTM parameter number 4 12 LSTM parameter number 48.
The null space is the set of all solutions to Ax 0. See full answer below. The number of parameters in a matrix is given by the difference between the number of columns present in the matrix and the rank of the matrix.
Consistent means either many solutions or unique solution. The same expression can be written as follows. Write i The number of elements ii The order of the matrix iii Write the elements a 22 a 23 a 24 a 34 a 43 a 44.
The OP has since added a second parameter. Find the number of parameters in the general solution of Ax 0 if A is a 5 x 6 matrix of rank 2. When multiplying two matrices the resulting matrix will have the same number of rows as the first matrix in this case A and the same number of columns as the second matrix BSince A is 2 3 and B is 3 4 C will be a 2 4 matrix.
The number of columns of the resulting matrix equals the number of columns of the second matrix. Iii a 22 means the element is in place 2nd row and second column. What is the nullity for A if the column vectors of A 4 x 4 are linearly independent.
R program to illustrate. Since the rank is the number of non zero rows there will be 4 zero rows the number of rows is 6 the rank is 2 another 4 are zero rows. Ii The order of matrix is 4 x 4.
Find the determinant Find the inverse Transpose Find the rank Multiply by Triangular matrix Diagonal matrix Raise to the power of LU-decomposition Cholesky decomposition 2 n 12 AXB A-1 123456729-1 adjugateA determinantA expA rankA transposeA AXB YAB sinA cosA logA arctanA svd A QR-decomposition A. We apply elementary row operations as follows. A logical value indicating whether the value should be returned as a factor of column labels created if necessary rather than as numbers.
To find the number of parameters you will need to go later by later and calculate the number of parameters used in the layer. A 1 2 1 1 1 1 1 1 a R 1 R 2 1 1 1 a 1 2 1 1 1 a R 3 R 1 R 2 a R 1 1 1 1 0 1 a 2 a 0 2 2 a R 2 R 3 1 1 1 0 2 2 a 0 1 a 2 a R 3 1 a 2 R 2 1 1 1 0 2 2 a 0 0 2 a a 1 2. Note that the matrix multiplication BA is not possible.
For each Gaussian you have.

Symbols Used Statistics And Parameters Statistics Math Life Hacks For School Ap Statistics
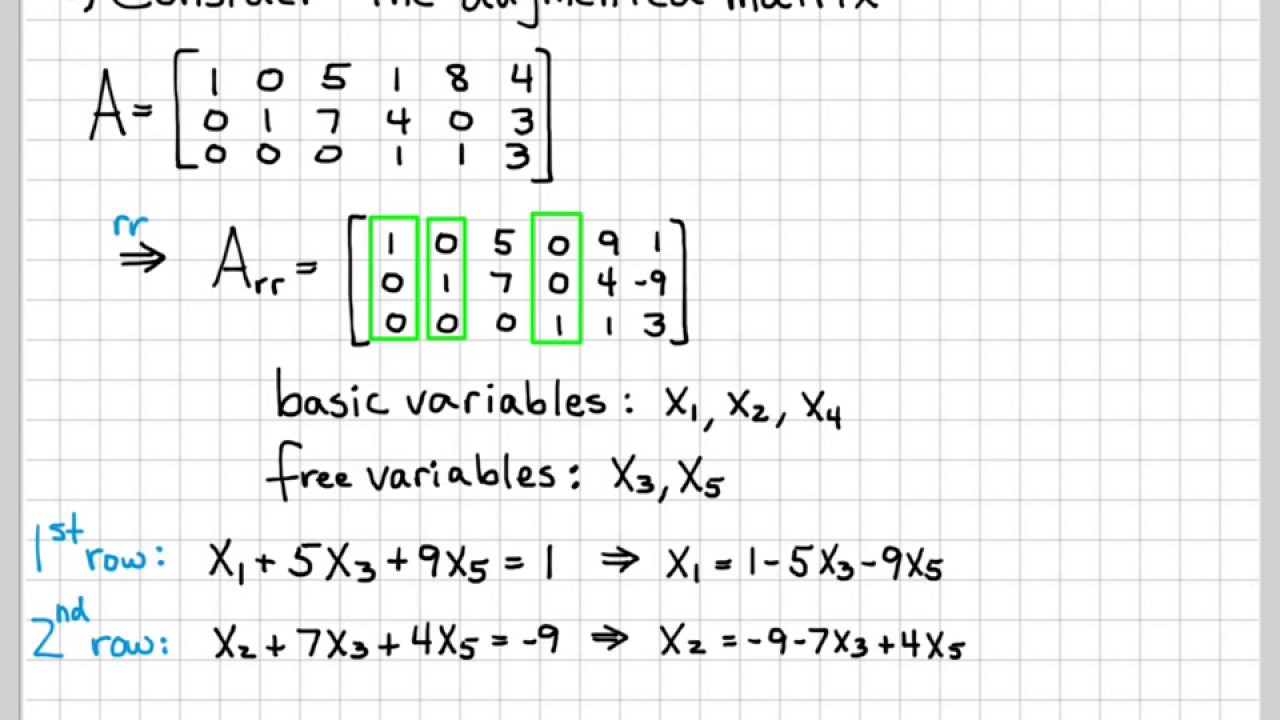
Linear Algebra Example Problems General Solution Of Augmented Matrix Youtube

Hcr S Formula Is The Simplest Way To Calculate All The Important Parameters Of Any Regular Polyhedron Just By Measurin Polyhedron Area And Perimeter Case Study

Solve System Of Linear Equations Using Excel Matrix Functions Linear Equations Equations College Algebra
0 Comments